题意概括:加上最少的括号,使原来的残缺括号串变成合法的括号串,我们称之为最小括号串,例如([)]变成()[()]
假设最后生成的最小括号串是唯一的,那么其中每一个括号字符都有与它配对的括号字符,那么我们的目标其实就是找出原残缺括号串中,已经存在的最小括号串中的括号配对,然后再补全缺少配对的括号。例如,下面图片中红色中括号是残缺括号串中已有配对:

对于一个左括号,在残缺括号串中可能会存在多个右括号可以与之匹配。但在最小括号串中,只有其中一个右括号,或干脆没有(如上例)右括号,与这个左括号匹配。对于一个右括号也是同理。
当我们选定一对括号成为一组配对时,原括号串将被划为两个区域,即“括号内”与“括号外”,分别在两个区域中的左右括号将无法组成括号串

对于一个合法括号串,一定是由一个或多个同级的最外层括号组成的,如下图


我们的只要在对应的局部残缺括号串中,找出这些最外层括号之间的分割点。
d[i][j] 代表 i~j残缺括号子串 所需要补充括号的最少数量。
对于i~j残缺括号子串,如果找到正确的最外层括号分割点,则“需要补充的括号数量”最少
public static void dp() {
for (int i = 0; i < len; i++) {
d[i][i] = 1; //只有一个括号字符,必定需要补上另一半
d[i+1][i] = 0; //已经是最里层的括号了
}
for(int start = len-2; start >= 0 ; start--) {
for(int end = start+1; end < len; end++) {
d[start][end] = len; // 最多增长为原来字符串的两倍
// 分割括号串 的情况
// 其实就是找出当前最外层括号对之间的分割点,正确的最外层分割点能让“需要补充的括号数量”最少
for(int k = start; k < end; k++) {
d[start][end] = Math.min(d[start][end], d[start][k] + d[k+1][end]);
}
// 不分割 且 两头刚好能组成一对括号的情况
// 如果两头不能组成一对括号,或者不是最优配对法,那么最优配对已经在前一种(分割)的情况里了
if(isBuddy(s[start], s[end])) {
d[start][end] = Math.min(d[start][end], d[start+1][end-1]);
}
}
}
}
未完待续 #
- 遍历顺序有讲究
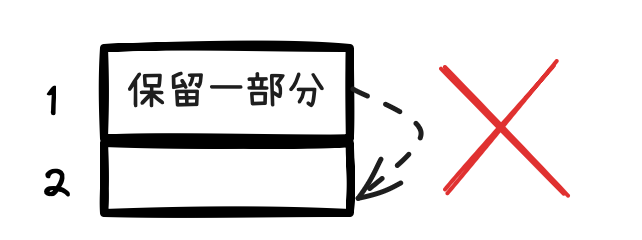
- 对于找不到配对的括号,最好的配对方法,就是直接在他相邻位置补上一个配对的括号,此时自然就变成了AB形式的括号串,也就是在每个合法括号串的最外层。所以最后一张图片是错误的